Convergence in Hartree-Fock Calculations
The convergence of Hartree-Fock SCF calculations depends on a series of options. All of these have sensible defaults which lead to usually well behaved SCF calculations. The most obvious parameter is the number of SCF cycles which can be set with
SCF=(MaxCycle=N)
the default being N=64. This default is sufficient for most systems, but significantly higher numbers are required for systems with closely spaced orbitals such as some transition metal complexes. The convergence criterion for rms deviations in electron density matrix elements of the SCF algorithm can be set directly by
SCF=(Conver=n)
the default for n being 8 for geometry optimization and frequency jobs and n=4 for single point calculations. The latter default is rarely appropriate and should be adjusted to the same value as for geometry optimizations. Using SCF=tight is synonymous with SCF=(Conver=8) and SCF=SinglePoint is synonymous with SCF=(Conver=4). The following table illustrates how much the number of SCF cycles varies with the SCF convergence criterion for the HF/STO-3G calculation on formaldehyde :
| Conver=n | optimization- cycles |
final energy (Hartree) |
|---|---|---|
| 4 | 6 | -112.354346245 |
| 5 | 7 | -112.354347141 |
| 6 | 8 | -112.354347141 |
| 7 | 9 | -112.354347141 |
| 8 | 10 | -112.354347141 |
| 9 | 11 | -112.354347141 |
One can clearly see that the total energy of the system is converged to within 10-9 Hartree already with SCF=(Conver=5) and that each increase in the convergence criterion is accompanied by an increase in the number of SCF cycles. For larger and for less well behaved systems the consequences of changing the convergence criterion are usually much more pronounced. Calculations on large systems can be accelerated substantially by lowering various cutoffs and convergence parameters using SCF=sleazy. This is particularly helpful in geometry optimizations when still far away from the minimum.
The initial guess used to start the SCF calculation is of great importance for both the efficiency as well as the final result obtained in the SCF calculation. The latter point is of particular importance in symmetric species in which the symmetry of the initial guess decides over the symmetry of the converged SCF wavefunction. Whether the symmetry of the initial guess is retained during SCF cycles depends on the version of Gaussian in use. Newer versions do NOT retain the symmetry of the initial guess unless SCF=Symm is specified. Using the NH2 radical as an example, we will see how either the 2A1 or the 2B1 states can be obtained at the ROHF/STO-3G level of theory depending on the initial guess being used. Starting the SCF calculation with the default (Harris) guess with:
#ROHF/STO-3G scf=(symm,tight)
rohf/STO-3G amide radical NH2, 2B1 state
0 2
N1
H2 1 r2
H3 1 r2 2 a3
r2=1.05726795
a3=100.0637224
|
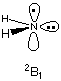 |
will give the following result:
Harris functional with IExCor= 205 diagonalized for initial guess.
ExpMin= 1.69D-01 ExpMax= 9.91D+01 ExpMxC= 9.91D+01 IAcc=1 IRadAn= 1 AccDes= 1.00D-06
HarFok: IExCor= 205 AccDes= 1.00D-06 IRadAn= 1 IDoV=1
ScaDFX= 1.000000 1.000000 1.000000 1.000000
Initial guess orbital symmetries:
Occupied (A1) (A1) (B2) (A1) (B1)
Virtual (A1) (B2)
The electronic state of the initial guess is 2-B1.
Requested convergence on RMS density matrix=1.00D-08 within 128 cycles.
Requested convergence on MAX density matrix=1.00D-06.
Requested convergence on energy=1.00D-06.
No special actions if energy rises.
Keep R1 and R2 integrals in memory in canonical form, NReq= 419815.
SCF Done: E(ROHF) = -54.8368134090 A.U. after 7 cycles
Convg = 0.5123D-11 -V/T = 2.0047
S**2 = 0.7500
Annihilation of the first spin contaminant:
S**2 before annihilation 0.7500, after 0.7500
**********************************************************************
Population analysis using the SCF density.
**********************************************************************
Orbital symmetries:
Occupied (A1) (A1) (B2) (A1) (B1)
Virtual (A1) (B2)
The electronic state is 2-B1.
The Harris functional guess predicts a highest (singly) occupied orbital of "(B1)" symmetry leading to a doublet 2B1 state in the converged wavefunction. The SCF algorithm retains the number of occupied orbitals in each irreducible representation (3*A1, 1*B2, 1*B1). The first unoccupied molecular orbital (LUMO) is of A1 symmetry. Interchange of the SOMO and LUMO will in this case lead to occupation of orbitals of different symmetry and thus to a different electronic state. Adjustment of the initial guess orbitals can be achieved with the guess=alter keyword and definition of the list of orbital exchanges after the geometry definition. In the following input orbitals 5 and 6 of the initial guess will be interchanged.
#ROHF/STO-3G scf=(symm,tight) guess=alter
rohf/STO-3G opt amide radical NH2, 2A1 state
0 2
N1
H2 1 r2
H3 1 r2 2 a3
r2=1.05726795
a3=100.0637224
5 6
|
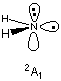 |
In some cases it might be advantageous to inspect the initial guess before actually doing an SCF calculation with guess=only and also to check the intended alterations with guess=(only,alter). With the SCF calculation for the 2B1 state in hand, we can compfortably skip this procedure. Here the SCF procedure gives the following final result:
Harris functional with IExCor= 205 diagonalized for initial guess.
ExpMin= 1.69D-01 ExpMax= 9.91D+01 ExpMxC= 9.91D+01 IAcc=1 IRadAn= 1 AccDes= 1.00D-06
HarFok: IExCor= 205 AccDes= 1.00D-06 IRadAn= 1 IDoV=1
ScaDFX= 1.000000 1.000000 1.000000 1.000000
Pairs of Alpha orbitals switched:
5 6
Initial guess orbital symmetries:
Occupied (A1) (A1) (B2) (A1) (A1)
Virtual (B1) (B2)
The electronic state of the initial guess is 2-A1.
Requested convergence on RMS density matrix=1.00D-08 within 128 cycles.
Requested convergence on MAX density matrix=1.00D-06.
Requested convergence on energy=1.00D-06.
No special actions if energy rises.
Keep R1 and R2 integrals in memory in canonical form, NReq= 419815.
SCF Done: E(ROHF) = -54.3257900934 A.U. after 9 cycles
Convg = 0.7698D-09 -V/T = 1.9800
S**2 = 0.7500
Annihilation of the first spin contaminant:
S**2 before annihilation 0.7500, after 0.7500
**********************************************************************
Population analysis using the SCF density.
**********************************************************************
Orbital symmetries:
Occupied (A1) (A1) (B2) (A1) (A1)
Virtual (B1) (B2)
The electronic state is 2-A1.
After performing the default Harris functional guess all orbital changes are listed (here only 5 and 6 are interchanged). This leads to an initial guess wavefunction with a SOMO of A1 symmetry. The relative order of orbital symmetries is retained during the SCF optimization and the final wavefunction therefore describes an 2A1 state. This wavefunction is stored in the checkpoint file on completion of the calculation and can be read from there as the initial guess for yet another calculation with guess=read. The following input file reads, for example the geometry as well as the wavefunction obtained in the previous calculation from the checkpoint file (here named /scr1/testit.chk) and calculates the ROHF/STO-3G energy within a single SCF cycle. Since the wavefunction stored in the checkpoint file is of 2A1 symmetry, the SCF will converge to the 2A1 state without any orbital interchanges.
%chk=/scr1/testit.chk
#ROHF/STO-3G scf=(symm,tight) guess=read geom=check
rohf/STO-3G opt amide radical NH2, 2A1 state
0 2
Comparison of the two states optimized here shows that the 2B1 state based on the default Harris functional guess is energetically more favorable at -54.8368134090 au than the 2A1 state at -54.3257900934 au. Thus, the default guess arrives at the electronically more favorable state. This is, however, not always the case.
Selection and manipulation of the initial guess for UHF wavefunctions is only slightly more challenging than that for the ROHF case. The added difficulty consists in deciding whether alpha or beta orbitals should be interchanged in order to arrive at the desired electronic state. For the current case of the NH2 radical, use of the default Harris functional guess yields again the energetically more favourable 2B1 state at -54.8392961557 au. Please note the ROHF/UHF energy lowering of only -0.0025au (-6.5 kJ/mol) in this case, suggesting that the wavefunction is well described already in the ROHF picture. The orbital listing obtained for the converged UHF wavefunction is:
SCF Done: E(UHF) = -54.8392961557 A.U. after 10 cycles
Convg = 0.4780D-08 -V/T = 2.0048
S**2 = 0.7585
Annihilation of the first spin contaminant:
S**2 before annihilation 0.7585, after 0.7500
**********************************************************************
Population analysis using the SCF density.
**********************************************************************
Orbital symmetries:
Alpha Orbitals:
Occupied (A1) (A1) (B2) (B1) (A1)
Virtual (A1) (B2)
Beta Orbitals:
Occupied (A1) (A1) (B2) (A1)
Virtual (B1) (A1) (B2)
The electronic state is 2-B1.
Comparison of the occupied alpha and beta spin orbitals shows that the additional alpha electron is located in an orbital of B1 symmetry. The complementary beta spin orbital is not occupied. Excitation of the electron in the highest lying beta orbital (A1 symmetry) to the next higher beta orbital (of B1 symmetry) changes the situation such that in both the alpha and beta orbitals there is one B1 and one B2 occupied orbital while the number of alpha orbitals with A1 symmetry exceeds that of the beta orbitals by one:
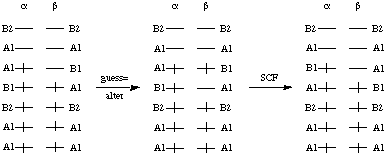
In order to effect the interchange of beta orbitals 4 and 5 the following input file will be used. Please observe the two empty lines after the geometry input. The first empty line terminates the geomtry input section, the second empty line specifies no changes in the alpha spin orbitals, and the following line specifies the changes in beta spin orbitals:
#UHF/STO-3G scf=(symm,tight) guess=alter
uhf/STO-3G opt amide radical NH2, 2A1 state
0 2
N1
H2 1 r2
H3 1 r2 2 a3
r2=1.05808265
a3=100.14734623
one empty line!!
a second empty line!!
4 5
final empty line!!!
The final orbital ordering obtained after the SCF in this case is:
SCF Done: E(UHF) = -54.7318269247 A.U. after 10 cycles
Convg = 0.6550D-08 -V/T = 2.0029
S**2 = 0.7508
Annihilation of the first spin contaminant:
S**2 before annihilation 0.7508, after 0.7500
**********************************************************************
Population analysis using the SCF density.
**********************************************************************
Orbital symmetries:
Alpha Orbitals:
Occupied (A1) (A1) (B2) (A1) (B1)
Virtual (A1) (B2)
Beta Orbitals:
Occupied (A1) (A1) (B2) (B1)
Virtual (A1) (A1) (B2)
The electronic state is 2-A1.
Please observe that the difference between the ROHF/STO-3G (at -54.3257900934 au) and the UHF/STO-3G (at -54.7318269247 au) energies of the 2A1 state is much larger at 1066 kJ/mol than found for the 2B1 state at the same theoretical levels.
There are two different SCF algorithms available in Gaussian. The default algorithm DIIS is quite fast and works well for most systems. For problematic cases the quadratically convergent (QC) algorithm is much more reliable but also much slower than DIIS. The latter option is used with the SCF=QC keyword and becomes quite usefull in the case of convergence problems with the default DIIS algorithm.
In the case of severe convergence problems, a few further strategies exist to approach the problem. As a first point it is important to check the geometry of the system under investigation. Errors in the Z-Matrix definition, which position atomic centers too close together, often result in convergence problems during SCF calculations. Also, it is often found that self consistency is achieved with one method, but not another. It is therefore quite helpful to calculate a wavefunction first with one method and then use the converged wavefunction as the initial guess for another calculation. It is, for example frequently found that Hartree-Fock calculations converge more readily than DFT calculations and initial calculation of the HF wavefunction can therefore aid in getting the DFT calculation started. Ultimately, the convergence behaviour also improves with reduced electron numbers. If, for example, calculations for neutral radicals do not converge, a converged wavefunction can often be obtained for the corresponding cationic systems (lacking one electron). The cation wavefunction can then be used as the initial guess of the radical system. If still no convergence can be achieved: go look for another project!