Following the Intrinsic Reaction Coordinate

In order to verify the nature of a transition state that has been optimized with one of the local methods described before, the Hessian needs to display the required number of negative eigenvalues. Aside from this local criterion, it is also necessary to identify the minima connected through the transition state. This latter part is usually performed through calculation of some kind of reaction coordinate. One particular choice is the intrinsic reaction coordinate (IRC), defined as the minimum energy reaction pathway (MERP) in mass-weighted cartesian coordinates between the transition state of a reaction and its reactants and products. It can be thought of as the path that the molecule takes moving down the product and reactant valleys with zero kinetic energy. The Gonzalez-Schlegel method for following the IRC can be used in Gaussian using the irc keyword.
 

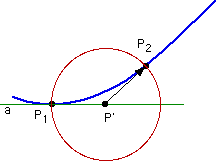
The "recipe" for following the IRC involves walking down the IRC in a number of steps with fixed step size n, each of them constructed in the following way: (1) Starting from point P1 on the path (shown in blue) construct auxiliary point P' located a distance of n/2 away from P1 along tangent a (shown in green). The construction of P' does not involve any energy or gradient calculations. (2) On a (hyper)sphere of radius n/2 centered at P' search for the point of lowest energy P2. This latter point is the new point on the IRC path. This constrained search requires several energy and gradient calculations and obeys the convergence criteria set with iop(1/7=x). (3)This sequence is repeated until the geometry convergence criteria are fulfilled in direction along the pathway.

The size of the IRC steps n is given in mass-weighted cartesian coordinates and can be set with

irc=(stepsize=n)

in units of 0.01 amu^-0.5Bohr, the default setting being n=10. If the step size is chosen too large, the constrained optimizations on the hypersphere will be difficult to converge, while a very small step size leads to a large number of IRC steps. The default step size is appropriate for many cases. A smaller step size such as n=3 is needed for systems with strongly curved IRC paths. For very flat potential energy surfaces the step size must be chosen such that the first steps away from the transition state reach a point at which the gradient has become large enough for the IRC to continue.

The structure of the transition state can either be given directly in the input file or (more often) be read from the checkpoint file of the previous transition state optimization using the

geom=check

keyword. In order to follow the IRC down from the transition state to the products, the second derivative matrix (Hessian) needs also to be known at the starting point. This information can either be retrieved from the checkpoint file (in case it has been calculated before) with

irc=(rcfc)

or it can be calculated at the beginning of the IRC path with

irc=(calcfc)

The number of steps per job can be determined with

irc=(maxpoints=N)

with N being a positive integer. The default in this case is N=10, much larger values being impractical due to large file sizes and long runtimes. For each step on the IRC path, the algorithm performs a constrained optimization on a hypersphere, the radius of which is set to half the step size. The convergence criteria for these steps as well as those for final convergence of the IRC itself can be set in the usual way with

iop(1/7=n)

A meaningful choice for n is 300 (as in normal geometry optimization calculations), smaller values being useful for flat potential energy surfaces. A tighter convergence criterion is also needed if small step sizes are used. Please observe that a tight convergence criterion can be specified either through iop(1/7=10) or through irc=(tight). The latter option is, however, not properly operating in some versions of Gaussian. Similarly, if left unspecified, the default geometry convergence criterion for IRC calculations in some versions of Gaussian is set to iop(1/7=3000). As this is rarely useful, it is important to always specify a convergence criterion explicitly in IRC calculations.

The direction of the IRC path can be chosen with either

irc=forward or irc=reverse

the forward direction corresponding to the direction of the transition vector with the largest component being positive. In practice it is often required to follow the IRC in both directions anyway and two separate calculations are used, one in the forward and one in the reverse direction. IRC calculations that have exhausted their maximum number of steps can be restarted with

irc=(restart,maxpoints=n)

with a larger number of maxpoints as before.

How these options can be put to work and what kind of errors are typically encountered will be demonstrated for the Huisgen reaction (dipolar cycloaddition reaction) of acetylene with hydrazoic acid as a worked example.