Performance in Hartree-Fock Calculations
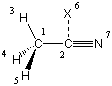
In traditional SCF calculations, the one- and two-electron integrals usually are first calculated and stored on disk before the electronic energy is minimized by variation of the molecular orbital coefficients. This type of calculation can be performed with SCF=Conventional. Please observe that the disk space required for "normal" inorganic and organic molecules and "typical" basis sets can quickly reach several GB! The default SCF procedure in Gaussian and many other programs is the direct SCF procedure in which only the one-electron integrals are computed and saved (on disk or in memory) while the two-electron integrals are recomputed for each SCF cycle (SCF=direct). Due to the better scaling of the direct SCF algorithm with system size, this method becomes faster than conventional SCF on most platforms already for moderately sized molecules. A third option termed SCF=incore keeps all calculated one- and two-electron integrals in main memory during SCF iterations. This is usually the fastest method available and is the default on systems with abundant main memory. In order to illustrate the results obtained with these three alternatives, we will resort to C3v symmetric acetonitrile in its HF/6-31G(d) structure and recompute its energy with a larger basis set (times in seconds on Pentium 4 LINUX PCs, 1GB main memory, scf=(conver=8)):
#P HF/6-311+G(d,p) scf=(conventional,conver=8)
HF/6-311+G(d,p)//HF/6-31G(d) sp acetonitrile (C3v)
0 1
C1
C2 1 r2
H3 1 r3 2 a3
H4 1 r3 2 a3 3 120.0
H5 1 r3 2 a3 3 -120.0
X6 2 1.0 1 90.0 3 0.0
N7 2 r7 6 90.0 1 180.0
r2=1.46783503
r3=1.08212473
r7=1.13472349
a3=109.83442501
|
 |
| algorithm | HF/6-311+G(d,p)- basis |
HF/6-311++G(2d,p)- basis |
6-311++G(3df,3pd)- basis |
|---|---|---|---|
| conventional | 6.5 | 12.1 | 80.8 |
| direct | 14.3 | 29.4 | 183.8 |
| incore | 5.3 | 10.9 | - |
While all of the conventional and direct calculations can be performed with the default memory allocation of 6MW (specified through %mem=6000000), the incore calculations require 8MW and 19MW, respectively, for the calculations using the 6-311+G(d,p) and the 6-311++G(2d,p) basis sets. Calculation of the single point energy at the HF/6-311++G(3df,3pd) level is not possible anymore with the incore algorithm on a computer with only 1 GB of main memory. For this small model system the incore algorithm outperforms the conventional SCF algorithm slightly while the direct SCF algorithm is much slower.
Aside from the choice of the SCF algorithm the run times for single point energy calculations on LINUX PCs also depends on other factors such as the CPU load caused by other processes as well as the amount of main memory specified through the %mem= directive. For the conventional SCF algorithm the following run times are obtained as a function of the main memory specification, again using the acetonitrile example at the HF/6-311+G(d,p) level of theory.
| %mem= [MW] | 6 | 8 | 16 | 32 | 64 | 96 |
| CPU [s] | 6.5 | 6.6 | 7.4 | 8.8 | 11.6 | 14.6 |
It can clearly be seen that for a given algorithm the CPU times increase with increasing memory, at least on a LINUX PC platform. Increasing the default memory specification thus only makes sense if a faster algorithm can be used (e.g. changing from direct to incore).
Attempted calculation of a similar series of Hartree-Fock energies for the alanylalanine dipeptide (HF/6-31G(d) structure here) gives the following results:
|
 |
Use of the incore algorithm is in this case restricted to the STO-3G, 3-21G, and 6-31G basis sets as main memory requirements exceed that available (1GB) beyond this point. Up to this point, however, the incore algorithm is the most efficient. The conventional algorithm is more efficient than the direct option for the small basis sets, but the direct algorithm becomes more competitive with larger basis sets. Calculations with the conventional algorithm will eventually also face the problem of not having enough hard disc space. This leaves us with the direct algorithm as the sole option for doing large scale Hartee-Fock calculations.