Population Analysis - where really are these electrons?

The methods used for analyzing the electron density of molecular systems can be divided up in three groups:

Methods based on the wave function (Mulliken Population Analysis, Natural Population Analysis)
Methods based on fitting the molecular electrostatic potential (such as the CHELPG and Merz-Singh-Kollman (MK) scheme)
Methods based on the electron density (such as AIM)

Due to the fundamental problem of deciding where atoms in a molecule actually start and where they end there is, however, no exact atomic charge. Nevertheless, the calculation of atomic charges is still quite helpful, be it for the use as an effective parameter in force field calculations or for the comparison of the chemical properties of two closely related systems.

Formal vs. partial charges
In particular when comparing two related systems it is important to keep in mind that the formal charges used frequently in molecular Lewis structures have nothing to do with actual atomic charges derived by one of the three approaches mentioned above. The ammonium cation (NH₄⁺) can be used to illustrate this point.

This latter system carries a positive formal charge on the nitrogen atom in order to indicate that the number of valence electrons formally located at the nitrogen center (4) is one less than the number of valence electrons in the nitrogen atom itself (5). Optimization of the ammonium cation at the Becke3LYP/6-31G(d) level of theory yields, as expected, a tetrahedral structure. The charge distribution can be calculated at the same level of theory using four different methods and the following charges for the central nitrogen atom are obtained:

Method	q(N)
Mulliken	-0.844
NPA	-0.977
CHELPG	-0.737
MK	-0.790

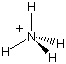Even though the four methods chosen here predict somewhat different amounts of negative charge on the nitrogen atom, they all agree that the nitrogen atom is a center of negative charge (the overall positive charge of the ammonium cation being distributed over the four adjacent hydrogen atoms).

Comparison of the above results with those obtained for (neutral) ammonia at the same level of theory shows that protonation of the nitrogen atom does indeed lead to a reduction of the negative partial charge of the nitrogen atom. The amount of the reduction is, however, much smaller than that suggested by the conversion of a formally neutral center to a positive one.

Method	q(N)
Mulliken	-0.888
NPA	-1.109
CHELPG	-1.017
MK	-1.024

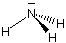The above results are by no means exceptions but reflect the normal situation in molecules containing electronegative elements such as nitrogen, oxygen, or halogens. These latter elements are only very rarely positively charged, even if the formal Lewis structures would suggest the opposite.

Specification of the density
When analysing the results from Hartree-Fock or DFT calculations, the density analyzed by one of the three methods mentioned above is by default the one described by the self-consistent orbitals optimized at that level. For electronic structure methods involving some sort of explicit electron correlation treatment such as MPn, QCI or CC, this is not the only choice. In the latter case one could either use the electron density as described by the Hartree-Fock orbitals or the density for the current method. While the former is selected with density=SCF, the latter is chosen with density=current. Using the example of ammonia in its Becke3LYP/6-31G(d) structure as above, the following results are obtained:

Method	density=	q(N,Mull.)	q(N,NPA)	q(N,CHELPG)
HF	SCF	-0.9852	-1.1147	-1.0634
HF	current	-0.9852	-1.1147	-1.0634
MP2(FC)	SCF	-0.9852	-1.1147	-1.0634
MP2(FC)	current	-0.9475	-1.1156	-1.0607

In this particular example the differences between Hartree-Fock density and MP2(FC) density are apparently small enough to yield rather similar results for the nitrogen partial charge with all three population analysis methods.

Open shell systems
In open shell systems the alpha- and beta-spin orbitals are not identical and population analyses can thus be performed separately for both densities. While accumulation of alpha- and beta-spin densities over atoms (following one of the established schemes) still yields atomic charges, the difference between alpha- and beta-spin densities corresponds to the unpaired spin density (SD) at a given center x:

SD_x = q(alpha)_x - q(beta)_x

In the case of the Mulliken population analysis, the atomic spin density values are automatically computed for open shell systems and printed to the output file. For doublet systems the sum of all atomic spin density values should equate exactly to 1.0. The spin densities should, of course, be highest at the formal radical center of a given species. For the NPA scheme the atomic alpha- and beta-spin densities are combined with half of the nuclear charge to yield the corresponding "Natural Charge" of alpha- and beta-type:

NPA(alpha)_x = q(nuc)_x/2 - q(alpha)_x

NPA(beta)_x = q(nuc)_x/2 - q(beta)_x

The unpaired spin densities SD_x can be obtained from these values according to:

SD_x = NPA(beta)_x - NPA(alpha)_x