Optimization of Symmetric Systems
Geometry optimization of the input structure being the default for any calculation with MOPAC, there is no particular need to add any keywords for the geometry optimization to work at all. In case symmetry restrictions should be imposed on the optimization process, this information must be provided in addition to the actual starting structure and the SYMMETRY keyword must be added to force the use of symmetry information. The symmetry relations are added directly after the geometry definition in the format:
(defining center),(symmetry relation),(defined center 1),(defined center 2) . . .
The internal coordinate symmetry relations are given as integers with the following meaning (only the most relevant relations are shown):
1 equal bond lengths
2 equal bond angles
3 equal dihedral angles
14 dihedral angle varies as the negative of reference dihedral angle
15 bond length varies as half of the reference bond length
16 bond angle varies as half of the reference bond angle
17 bond angle varies as 180 - reference bond length
Several examples will be used to illustrate the formal definition of symmetry relations.
1) water (C2v)
The following input file describes the full C2v symmetry of water:
AM1 PRECISE EF T=48H SYMMETRY
AM1 optimization of water in full C2v symmetry
O 0.00000000 0 0.0000000 0 0.0000000 0 0 0 0
H 1.00000000 1 0.0000000 0 0.0000000 0 1 0 0
H 1.00000000 1 105.0000000 1 0.0000000 0 1 2 0
2,1,3
|
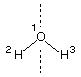 |
Here only one symmetry relation is necessary that relates the bond length of H2 to the bond length of H3 using symmetry relation 1. Please observe that the symmetry definitions must be separated from the actual geometry definition by one blank line and that another blank line must be added to terminate the symmetry input section. If given correctly in the input file, all symmetry relations will be listed at the beginning of the output file under the PARAMETER DEPENDENCE DATA heading.
2) hydrogen peroxide (C2)
The following input file describes the full C2 symmetry of hydrogen peroxide:
AM1 PRECISE EF T=48H SYMMETRY
AM1 optimization of H2O2 (C2)
XX 0.00000000 0 0.0000000 0 0.0000000 0 0 0 0
XX 1.00000000 0 0.0000000 0 0.0000000 0 1 0 0
O 0.650 1 90.0000000 0 0.0000000 0 2 1 0
O 0.650 1 90.0000000 0 180.0000000 0 2 1 3
H 0.983 1 105.96 1 63.94 1 3 2 1
H 0.983 1 105.96 1 63.94 1 4 2 1
3,1,4
5,1,6
5,2,6
5,3,6
|
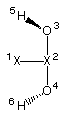 |
In this particular case two dummy atoms (symbolized as XX) are used to define the principal C2 axis of the system and all variables are subsequently defined relative to these two centers. The symmetry relations first define the equality of bond distances for the oxygen and hydrogen atoms (symmetry relation 1) and then equal bond angles and dihedral angles for the hydrogen atoms (symmetry relations 2 and 3).
3) methanol (Cs)
The following input file describes the full Cs symmetry of methanol:
AM1 PRECISE EF T=48H SYMMETRY
AM1 optimization of methanol (Cs)
H 0.00000000 0 0.0000000 0 0.0000000 0 0 0 0
C 1.11900000 1 0.0000000 0 0.0000000 0 1 0 0
O 1.410 1 105.1300000 1 0.0000000 0 2 1 0
H 0.964 1 107.1700000 1 180.0000000 0 3 2 1
H 1.119 1 110.94 1 -118.91 1 2 3 1
H 1.119 1 110.94 1 118.91 1 2 3 1
5,1,6
5,2,6
5,14,6
|
 |
One part of the symmetry information is given in this case as part of the Z-Matrix definition in that the dihedral angle for hydrogen atom 4 is set to 180.0 degrees and is not allowed to vary. The atoms 1 through 4 are thus all located in the principal plane of the system. Only atoms H5 and H6 extend below and above the plane and their bond distances, angles, and dihedral angles are related to each other. Please observe that the dihedral angle of H6 varies as the negative of the dihedral angle of H5 (symmetry relation 14).
In contrast to geometry optimizations with Gaussian, point group changes during geometry optimization will not be detected in MOPAC and will therefore not lead to termination of program execution.