The C_2v Point Group

This point group contains four symmetry operations:

E the identity operation
C₂ a twofold symmetry axis
σ_v the first mirror plane (xz)
σ_v' the second mirror plane (yz)

A simple example for a C₂v symmetric molecule is formaldehyde (CH₂O), here in its HF/6-31G(d) optimized structure:

#P HF/6-31G(d) opt=(Z-Matrix,tight) test1 HF/6-31G(d) opt formaldehyde 0 1 C1 O2 1 r2 H3 1 r3 2 a3 H4 1 r3 2 a3 3 180.0 r2=1.18435117 r3=1.09162067 a3=122.159223

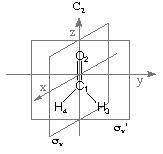In this case the symmetry of the system is reflected in the Z-Matrix only through the use of identical variable names for hydrogen atoms H3 and H4 and through constraining all atoms into one plane. This reduces the number of independent structural variables from 6 (for an asymmetric, non-linear molecule containing four centers) to 3.

Molecular orbitals as well as harmonic vibrations (if calculated) are labeled according to their symmetry properties as belonging to one of the four irreducible representations (A₁, A₂, B₁, and B₂) of the C_2v point group.