The C_i Point Group

This point group contains only two symmetry operations:

E the identity operation
i inversion through a center of symmetry

A simple example for a C_i symmetric molecule is 1,2-dichloro-1,2-difluoroethane (C₂H₂Cl₂F₂) in its staggered conformation displaying an anti-conformation of chloro and fluoro substituents. Here the HF/6-31G(d) optimized structure:

#P HF/6-31G(d) opt=(Z-Matrix,tight) HF/6-31G(d) opt Ci 1,2-dichloro-1,2-difluoroethane 0 1 X1 X2 1 1.0 C3 1 r3 2 90.0 C4 1 r3 2 90.0 3 180.0 Cl5 3 r5 1 a5 2 0.0 Cl6 4 r5 1 a5 2 180.0 F7 3 r7 5 a7 4 d7 F8 4 r7 6 a7 3 -d7 H9 3 r9 5 a9 7 d9 H10 4 r9 6 a9 8 -d9 r3=0.76028393 r5=1.76952333 r7=1.33959357 r9=1.0756268 a5=109.90682422 a7=108.83907475 a9=108.10703625 d7=-118.8835108 d9=-119.39438847

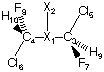In this case the symmetry of the system is reflected in the Z-Matrix through positioning of dummy atom X1 at the center of inversion (also the origin of the coordinate system), and the use of identical variables for the positioning of identical pairs of atoms. This reduces the number of independent structural variables from 18 (for an asymmetric, non-linear molecule containing eight centers) to 9.

Molecular orbitals as well as harmonic vibrations (if calculated) are labeled according to their symmetry properties as belonging to one of the two irreducible representations (A_g and A_u) of the C_i point group. Those properties belonging to irreducible representation A_g are symmetric to both the identity operation E as well as reflection through the center of inversion. Those properties belonging to irreducible representation A_u are symmetric with respect to the identity operation E but antisymmetric with respect to reflection through the center of inversion.