Information on Molecular Orbitals in the Gaussian output file
How much information on molecular orbitals is written to the Gaussian output file depends on the value of the Population or pop keyword. If no particular value is given, only the orbital energies (in atomic units) are printed. This is equivalent to pop=minimal. Selected information on the actual orbitals is obtained using pop=regular. Using this choice, information on the five highest occupied and the lowest five uncoccupied (virtual) orbitals are printed. This is, of course, only possible if there actually ARE at least five occupied and five virtual orbitals. In the following example of the HF/STO-3G orbitals of formaldehyde (CH2O, C2v point group):
#P HF/STO-3G scf=tight pop=regular
HF/STO-3G//HF/STO-3G sp formaldehyde
0 1
C1
O2 1 r2
H3 1 r3 2 a3
H4 1 r3 2 a3 3 180.0
r2=1.21672286
r3=1.10137241
a3=122.73666566
|
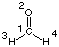 |
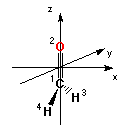
there are only four virtual orbitals and only those are printed. The orbital coefficients are given with respect to the molecule in its "Standard orientation" given at the beginning of the output file. The system is oriented such that the principal axis of the systems runs along the z-axis and that all atoms of the system are located in the yz-plane:
Standard orientation:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 6 0 0.000000 0.000000 -0.533912
2 8 0 0.000000 0.000000 0.682811
3 1 0 0.000000 0.926436 -1.129510
4 1 0 0.000000 -0.926436 -1.129510
---------------------------------------------------------------------
|
 |
The output starts with a listing of the orbital symmetries of all orbitals of the system. In this particular example, the highest occupied molecular orbital (HOMO) is orbital No. 8 and belongs to the B2 irreducible representation (antisymmetric with respect to the principal C2 axis). Following this information, the orbital energies of all orbitals of the system are given. For open shell systems the energies of the alpha electrons are given first, followed by the energies of the beta orbitals:
Orbital symmetries:
Occupied (A1) (A1) (A1) (A1) (B2) (A1) (B1) (B2)
Virtual (B1) (A1) (B2) (A1)
The electronic state is 1-A1.
Alpha occ. eigenvalues -- -20.31271 -11.12507 -1.33744 -0.80775 -0.63291
Alpha occ. eigenvalues -- -0.54553 -0.44319 -0.35438
Alpha virt. eigenvalues -- 0.28199 0.62863 0.73441 0.91294
Molecular Orbital Coefficients
4 5 6 7 8
(A1)--O (B2)--O (A1)--O (B1)--O (B2)--O
EIGENVALUES -- -0.80775 -0.63291 -0.54553 -0.44319 -0.35438
1 1 C 1S -0.18562 0.00000 0.03301 0.00000 0.00000
2 2S 0.57741 0.00000 -0.10669 0.00000 0.00000
3 2PX 0.00000 0.00000 0.00000 0.60936 0.00000
4 2PY 0.00000 0.53318 0.00000 0.00000 -0.18209
5 2PZ -0.22623 0.00000 -0.44751 0.00000 0.00000
6 2 O 1S 0.09884 0.00000 -0.09381 0.00000 0.00000
7 2S -0.42913 0.00000 0.49909 0.00000 0.00000
8 2PX 0.00000 0.00000 0.00000 0.67586 0.00000
9 2PY 0.00000 0.44231 0.00000 0.00000 0.86991
10 2PZ -0.16466 0.00000 0.67688 0.00000 0.00000
11 3 H 1S 0.26455 0.30023 0.15895 0.00000 -0.35921
12 4 H 1S 0.26455 -0.30023 0.15895 0.00000 0.35921
9 10 11 12
(B1)--V (A1)--V (B2)--V (A1)--V
EIGENVALUES -- 0.28199 0.62863 0.73441 0.91294
1 1 C 1S 0.00000 -0.20803 0.00000 -0.09478
2 2S 0.00000 1.30304 0.00000 0.63168
3 2PX 0.82111 0.00000 0.00000 0.00000
4 2PY 0.00000 0.00000 1.14840 0.00000
5 2PZ 0.00000 -0.44498 0.00000 1.17315
6 2 O 1S 0.00000 0.02810 0.00000 0.11577
7 2S 0.00000 -0.16145 0.00000 -0.86387
8 2PX -0.76729 0.00000 0.00000 0.00000
9 2PY 0.00000 0.00000 -0.31860 0.00000
10 2PZ 0.00000 0.24606 0.00000 0.92393
11 3 H 1S 0.00000 -0.88929 -0.83986 0.15471
12 4 H 1S 0.00000 -0.88929 0.83986 0.15471
|
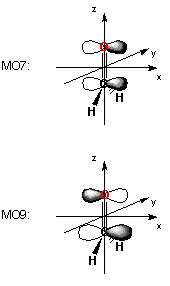 |
In the next section of output, the orbital coefficients are given first for the five highest occupied molecular orbitals. The header for each orbital includes the orbital symmetry, the label "O" for occupied or "V" for virtual orbitals, and the orbital energies in atomic units. The molecular orbital coefficients for the basis functions are then given in the order in which they appear in the basis set description (as obtained, for example, with the gfinput keyword). Orbital 7 listed in the formaldehyde example with an orbital energy of -0.44319 au is of B1 symmetry and composed exclusively of the 2px basis functions on carbon atom 1 and oxygen atom 2. This corresponds to the occupied pi-type molecular orbital of the C-O double bond. It is interesting to note that, in contrast to many textbook examples, this is not the highest occupied molecular orbital (HOMO) of this system. The latter (orbital 8 with an orbital energy of -0.35438 au) is mainly composed of the 2py basis functions on oxygen atom 2 and can best be thought of as an oxygen centered lone pair. The lowest unoccupied molecular orbital (LUMO) of the system is orbital 9 with an orbital energy of +0.28199 au and main contributions from the 2px basis functions on carbon atom 1 and oxygen atom 2, now with opposite sign. This is in line with expectations for the unoccupied pi* orbital of the C-O double bond.
Information on all orbitals of the system can be obtained with the pop=full keyword. Remember that the number of occupied orbitals is independent, but the number of virtual orbitals is strongly dependent on the number of basis functions. A full listing of all molecular orbitals can therefore become quite extensive for large basis set calculations on larger systems. This is particularly relevant for Gaussian as pop=full also forces a full Mulliken population analysis.
When moving away from minimal basis sets, the analysis of molecular orbital coefficients becomes more difficult, as there are many more basis functions (and therefore MO coefficients) than classical atomic orbitals. This is readily demonstrated using the HF/6-311G(d,p) orbitals of formaldehyde (HF/STO-3G structure) as an example:
Orbital symmetries:
Occupied (A1) (A1) (A1) (A1) (B2) (A1) (B1) (B2)
Virtual (B1) (A1) (B2) (A1) (A1) (B2) (B1) (B2) (A1) (A1)
(A1) (B1) (B2) (A2) (B1) (A1) (A1) (B2) (B2) (A1)
(B1) (A2) (A1) (B2) (B2) (A1) (A1) (B1) (A2) (A1)
(B1) (A1) (B2) (B2) (A1) (B1) (B2) (A1) (A1) (A1)
The electronic state is 1-A1.
Alpha occ. eigenvalues -- -20.57126 -11.34192 -1.39677 -0.87126 -0.68760
Alpha occ. eigenvalues -- -0.64756 -0.52789 -0.44085
Alpha virt. eigenvalues -- 0.12516 0.15625 0.21077 0.33039 0.47943
Alpha virt. eigenvalues -- 0.55866 0.57437 0.74085 0.80110 0.85841
Alpha virt. eigenvalues -- 0.98667 1.09706 1.15224 1.24623 1.50263
Alpha virt. eigenvalues -- 1.55040 1.64320 1.65415 1.84157 1.88722
Alpha virt. eigenvalues -- 2.02403 2.11540 2.40847 2.60635 2.73802
Alpha virt. eigenvalues -- 2.75352 2.83229 2.95131 3.25505 3.26831
Alpha virt. eigenvalues -- 3.69981 3.73483 3.80946 4.10219 4.21669
Alpha virt. eigenvalues -- 5.39516 5.50403 6.06721 24.98550 51.59020
Molecular Orbital Coefficients
4 5 6 7 8
(A1)--O (B2)--O (A1)--O (B1)--O (B2)--O
EIGENVALUES -- -0.87126 -0.68760 -0.64756 -0.52789 -0.44085
1 1 C 1S -0.08789 0.00000 0.01245 0.00000 0.00000
2 2S -0.14713 0.00000 0.02091 0.00000 0.00000
3 2PX 0.00000 0.00000 0.00000 0.14230 0.00000
4 2PY 0.00000 0.17912 0.00000 0.00000 -0.08342
5 2PZ -0.08046 0.00000 -0.16684 0.00000 0.00000
6 3S 0.40144 0.00000 -0.07991 0.00000 0.00000
7 3PX 0.00000 0.00000 0.00000 0.23992 0.00000
8 3PY 0.00000 0.27845 0.00000 0.00000 -0.14032
9 3PZ -0.11437 0.00000 -0.26911 0.00000 0.00000
10 4S 0.25737 0.00000 0.04616 0.00000 0.00000
11 4PX 0.00000 0.00000 0.00000 0.19312 0.00000
12 4PY 0.00000 0.13653 0.00000 0.00000 -0.02694
13 4PZ -0.06713 0.00000 -0.06445 0.00000 0.00000
14 5D 0 -0.00393 0.00000 -0.03003 0.00000 0.00000
15 5D+1 0.00000 0.00000 0.00000 0.05175 0.00000
16 5D-1 0.00000 0.00256 0.00000 0.00000 0.06960
17 5D+2 -0.01407 0.00000 -0.01274 0.00000 0.00000
18 5D-2 0.00000 0.00000 0.00000 0.00000 0.00000
19 2 O 1S 0.04656 0.00000 -0.03712 0.00000 0.00000
20 2S 0.07868 0.00000 -0.06286 0.00000 0.00000
21 2PX 0.00000 0.00000 0.00000 0.22120 0.00000
22 2PY 0.00000 0.15228 0.00000 0.00000 0.25178
23 2PZ -0.06544 0.00000 0.23348 0.00000 0.00000
24 3S -0.23278 0.00000 0.19078 0.00000 0.00000
25 3PX 0.00000 0.00000 0.00000 0.34693 0.00000
26 3PY 0.00000 0.23957 0.00000 0.00000 0.38028
27 3PZ -0.09897 0.00000 0.34271 0.00000 0.00000
28 4S -0.24010 0.00000 0.29517 0.00000 0.00000
29 4PX 0.00000 0.00000 0.00000 0.31869 0.00000
30 4PY 0.00000 0.17597 0.00000 0.00000 0.39654
31 4PZ -0.06410 0.00000 0.25624 0.00000 0.00000
32 5D 0 0.00611 0.00000 -0.02418 0.00000 0.00000
33 5D+1 0.00000 0.00000 0.00000 -0.02843 0.00000
34 5D-1 0.00000 -0.01934 0.00000 0.00000 -0.00994
35 5D+2 0.00124 0.00000 -0.00092 0.00000 0.00000
36 5D-2 0.00000 0.00000 0.00000 0.00000 0.00000
37 3 H 1S 0.10699 0.10980 0.05586 0.00000 -0.09884
38 2S 0.15467 0.16948 0.08015 0.00000 -0.21991
39 3S 0.00544 0.04175 0.03555 0.00000 -0.12090
40 4PX 0.00000 0.00000 0.00000 0.00794 0.00000
41 4PY -0.02106 -0.01486 -0.00908 0.00000 0.00414
42 4PZ 0.00944 0.01004 -0.00358 0.00000 -0.00727
43 4 H 1S 0.10699 -0.10980 0.05586 0.00000 0.09884
44 2S 0.15467 -0.16948 0.08015 0.00000 0.21991
45 3S 0.00544 -0.04175 0.03555 0.00000 0.12090
46 4PX 0.00000 0.00000 0.00000 0.00794 0.00000
47 4PY 0.02106 -0.01486 0.00908 0.00000 0.00414
48 4PZ 0.00944 -0.01004 -0.00358 0.00000 0.00727
|
 |
Molecular orbital 8 (the HOMO) is now described by as much as 48 MO coefficients, each of the two hydrogen atoms contributing 6, and carbon and oxygen contributing 18 basis functions. With this increased flexibility of the basis set, the ease of interpretation of the single MO coefficients is almost completely lost. In this situation, analysis of the orbital structure using one of the population analysis schemes (Mulliken population analysis, Natural Population Analysis, AIM . . ) or simly plotting the molecular orbitals in 2D- or 3D-diagrams is clearly preferrable.