Los Alamos National Laboratory (LANL) effective core potentials
This type of pseudo-potential is available for a variety of elements together with the appropriate valence basis set. The latter is of double zeta (DZ) quality and the overall combination of ECP and valence basis set is thus referred to as "LANL2DZ" basis (W. R. Wadt, P. J. Hay, J. Chem. Phys., 1985, 82, 270 + 284 + 299). LANL2 ECPs have not been defined for elements H - Ne and the all-electron valence double zeta basis sets developed by Dunning (D95V) are used for these elements instead. The ECP parameters for elements Na - Kr have been derived from atomic wavefunctions obtained in all-electron non-relativistic Hartree-Fock calculations, while relativistic Hartree-Fock calculations have been used for the heavier elements Rb - Bi.
Using the halogens as a first example, the situation is as follows for the elements F, Cl, Br, and I (explicitly treated electrons are labeled in blue, those treated by ECPs are labeled in black):
| element | core configuration |
core electrons |
valence configuration |
valence electrons |
valence basis set |
|---|---|---|---|---|---|
| F | 1s | 2 | 2s2p | 7 | D95V |
| Cl | 1s2s2p | 10 | 3s3p | 7 | D95 |
| Br | 1s2s2p3s3p3d | 28 | 4s4p | 7 | D95 |
| I | 1s2s2p3s3p3d4s4p4d | 46 | 5s5p | 7 | D95 |
The use of ECP + valence basis set combinations in geometry optimizations leads to similar results as compared to all electron basis sets of comparable quality. The following table compiles results for methyl halides CH3-X (X=F, Cl, Br, I) as optimized at B3LYP and MP2(FC) level. It is easily seen from these results that unpolarized valence basis sets (with or without ECPs) are not well suited to reproduce experimentally measured C-X bond lengths. Addition of a single set of d-type polarization functions on carbon and halide X improves the predictive quality of the basis set significantly. The effects of additional diffuse functions on the halides are, in comparison, rather minor. It is only for chlorine that a direct comparison of all-electron calculations with the D95V basis set and the ECP calculations using the LANL2DZ combination can be made. At least for this system and the quantum mechanical methods chosen here there is no significant difference in the computed structures.
|
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [a] diffuse and polarization functions on halogens by Check et al., J. Phys. Chem. A, 2001, 105, 8111. [b] Demaison et al., Structural Chem., 1999, 10, 129. [c] Jensen et al., J. Mol. Spectr., 1981, 88, 378. [d] Graner et al., J. Mol. Spectr., 1981, 90, 394. [e] Demaison et al., Structural Chem., 2003, 14, 159. [f] polarization functions on halogens by Frenking et al., Chem. Phys. Lett., 1993, 208, 237. [g] polarization functions on halogens taken from the 6-31G(d) all-electron basis sets. [h] polarization functions on halogens taken from the D95(V) all-electron basis sets. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The differences between all-electron calculations and those using ECPs can be illustrated with the results obtained for octachlorohexatriene. This system can either exist as trans isomer T or as cis isomer C.
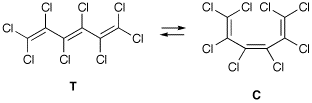
When optimization is performed at the (all-electron) B3LYP/6-31G(2d) level, the difference in total energy between these two systems amounts to 3.0 kJ/mol (favouring the trans isomer T). Replacing the 6-31G(2d) basis set on chlorine by the LANL2DZ ECP + valence basis combination while keeping the two d-type polarization functions from the 6-31G(2d) basis set, the energy difference is reduced to 2.0 kJ/mol (still favouring the trans isomer T). The computational effort required for the calculation of analytical second derivatives decreases significantly from 137 min for the all-electron to 75 min for the ECP case. The difference in all-electron vs ECP basis does, of course, also depend on the type of calculation performed.
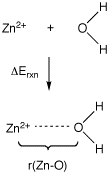
Use of LANL2DZ ECPs for metals is illustrated here with the reaction of Zn2+ with water, generating the monosolvated dication complex. While for the lighter elements the D95V all-electron basis is used, the LAN2DZ ECP replaces the innermost 18 electrons in Zn by an ECP and treats the remaining 12 electrons explicitly with a DZ basis. Explicitly treated electrons are again shown in blue, those treated by the ECP are shown in black:
| element | core configuration |
core electrons |
valence configuration |
valence electrons |
valence basis set |
|---|---|---|---|---|---|
| H | - | - | 1s | 1 | D95V |
| O | 1s | 2 | 2s2p | 6 | D95V |
| Zn | 1s2s2p3s3p | 18 | 3d4s | 12 | D95 |
Geometries and complexation energies for Zn2+(H2O) calculated with either all-electron or ECP + valence basis set combinations are collected in the following table. Partial charges for zinc q(Zn) have been calculated using the Natural Population Analysis (NPA) method.
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [a] polarization functions on zinc taken from the 6-31G(d) all-electron basis set. [b] polarization functions on zinc taken from the 6-311G(d) all-electron basis set. [c] diffuse and polarization functions on zinc taken from the 6-311+G(2d) all-electron basis set. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The all-electron calculations predict slightly shorter Zn - O bond distances than calculations using the LANL2DZ ECP. The charge parameters obtained for Zn are, however, largely identical for both approaches. More sophisticated basis sets have been developed for use in highly accurate calculations with correlated methods. A selection of relevant literature references is given here:
- J. M. L. Martin, A. Sundermann,
"Correlation consistent valence basis sets for use with the Stuttgart-Dresden-Bonn relativistic effective core potentials: the atoms Ga-Kr and In-Xe"
J. Chem. Phys. 2001, 114, 3408 - 3420. - D. Feller, K. A. Peterson, W. A. de Jong, D. A. Dixon,
"Performance of coupled cluster theory in thermochemical calculations of small halogenated compounds"
J. Chem. Phys. 2003, 118, 3510 - 3522.