8.1 Calculation of NMR Isotropic Shieldings
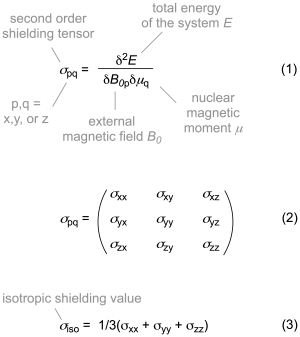
NMR chemical shifts in solution are directly related to the chemical shielding values (often abbreviated with the greek sigma symbol) of NMR active nuclei. As shown in eq. (1), the shieldings are defined as the second derivatives of the total energy with respect to the external magnetic field and the nuclear magnetic moments (in Cartesian coordinates). Most quantum chemical programs list the nine components of the shielding tensor in the block format shown in eq. (2) together with the isotropic shielding value calculated as the average of the three tensor diagonal elements. It is only under the conditions of fast directional averaging (gas or liquid phase) where the isotropic shielding is a usefuly quantity for the prediction of chemical shift values.
Shielding calculations are commonly performed on minimum energy structures of the systems under study (that is, after initial geometry optimization). In Gaussian the shielding calculations are performed for all NMR active nuclei with the "NMR" keyword as shown for the example of methane in Table 8.1.1 below.
Table 8.1.1. Input and relevant output file sections for NMR calculations with Gaussian for methane (CH4).
input file#P M062X/Def2TZVPP int=ultrafine NMR M06-2X/def2-TZVPP CH4 shieldings. 0 1 C 0.00000000 0.00000000 0.00000000 H 0.62766400 0.62766400 0.62766400 H -0.62766400 -0.62766400 0.62766400 H -0.62766400 0.62766400 -0.62766400 H 0.62766400 -0.62766400 -0.62766400 system
|
output file
Calculating GIAO nuclear magnetic shielding tensors.
SCF GIAO Magnetic shielding tensor (ppm):
1 C Isotropic = 194.2234 Anisotropy = 0.0000
XX= 194.2234 YX= 0.0000 ZX= -0.0000
XY= 0.0000 YY= 194.2234 ZY= -0.0000
XZ= 0.0000 YZ= -0.0000 ZZ= 194.2234
Eigenvalues: 194.2234 194.2234 194.2234
2 H Isotropic = 31.6000 Anisotropy = 9.6449
XX= 31.6000 YX= 3.2150 ZX= 3.2150
XY= 3.2150 YY= 31.6000 ZY= 3.2150
XZ= 3.2150 YZ= 3.2150 ZZ= 31.6000
Eigenvalues: 28.3850 28.3850 38.0299
3 H Isotropic = 31.6000 Anisotropy = 9.6449
XX= 31.6000 YX= 3.2150 ZX= -3.2150
XY= 3.2150 YY= 31.6000 ZY= -3.2150
XZ= -3.2150 YZ= -3.2150 ZZ= 31.6000
Eigenvalues: 28.3850 28.3850 38.0299
4 H Isotropic = 31.6000 Anisotropy = 9.6449
XX= 31.6000 YX= -3.2150 ZX= 3.2150
XY= -3.2150 YY= 31.6000 ZY= -3.2150
XZ= 3.2150 YZ= -3.2150 ZZ= 31.6000
Eigenvalues: 28.3850 28.3850 38.0299
5 H Isotropic = 31.6000 Anisotropy = 9.6449
XX= 31.6000 YX= -3.2150 ZX= -3.2150
XY= -3.2150 YY= 31.6000 ZY= 3.2150
XZ= -3.2150 YZ= 3.2150 ZZ= 31.6000
Eigenvalues: 28.3850 28.3850 38.0299
|
The gauge-including atomic orbital (GIAO) method used in Gaussian generates shielding values based on the SCF density of the underlying quantum mechanical method (here: M06-2X/def2-TZVPP). The results are reported in ppm for each of the NMR active nuclei in the order of appearance in the input coordinates. The first atom listed here is the methane carbon atom and the shieldings are those for the 13C isotope. Due to the Td symmetry of methane, all off-diagonal elements of the shielding tensor are zero and all diagonal elements have identical values (of 194.2234 ppm). The resulting isotropic shielding value for carbon atom C1 therefore amounts to 194.2234 ppm. It is furthermore satisfying to see that isotropic shielding values for all four (1H) hydrogen atoms are identical (due to Td symmetry) at 31.6000 ppm. The Linux grep command on "Isotropic =" can be used to extract a compact summary of all isotropic shieldings from the Gaussian output file.
Performing effectively the same calculation in ORCA 6.0 yields the results shown in Table 8.1.2. In order to keep things as similar as in Gaussian, the "NORI" keyword is used to supress fast integral calculations with the RI methodology. This is not necessarily meaningful in production NMR calculations. The ORCA output file features a more detailed block of information for the shielding calculations of each of the NMR active nuclei. For most purposes the "CHEMICAL SHIELDING SUMMARY" section is all we need for NMR chemical shift calculations. Again we see the shieldings to be identical for all four hydrogen atoms. However, comparing the results from ORCA with those from Gaussian we note significant differences for hydrogens (31.6000 vs. 31.337 ppm) as well as the carbon atom (194.2234 vs. 189.229 ppm), despite the fact that M06-2X/def2-TZVPP calculations were performed in both cases. Matching these values to the experimentally known shieldings from gas phase NMR measurements of methane[3] of 30.61 ppm for 1H and 195.1 ppm for 13C is of little help as absolute errors seem substantial in both cases. We will see later that accurate predictions of NMR chemical shifts depend very much on selecting an appropriate reference relative to which absolute shielding values will be compared.
Table 8.1.2. Input and relevant output file sections for NMR calculations with ORCA for methane CH4).
input file
! M062X NORI def2-TZVPP TightSCF defgrid3 NMR UseSym
%pal
nprocs 8
end
%scf
MaxIter 300
end
%maxcore 1000
* xyz 0 1
C 0.00000000 0.00000000 0.00000000
H 0.62766400 0.62766400 0.62766400
H -0.62766400 -0.62766400 0.62766400
H -0.62766400 0.62766400 -0.62766400
H 0.62766400 -0.62766400 -0.62766400
*
%eprnmr
NUCLEI = ALL H {SHIFT}
NUCLEI = ALL C {SHIFT}
end
|
output file
--------------------------------
CHEMICAL SHIELDING SUMMARY (ppm)
--------------------------------
Nucleus Element Isotropic Anisotropy
------- ------- ------------ ------------
1 H 31.337 9.331
2 H 31.337 9.331
3 H 31.337 9.331
4 H 31.337 9.331
0 C 189.229 0.000
system
|
References
[1] G. Schreckenbach, T. Ziegler, “Calculation of NMR Shielding Tensors Using Gauge-Including Atomic Orbitals and Modern Density Functional Theory”, J. Phys. Chem. 1995, 99, 606–611.
[2] R. K. Harris, E. D. Becker, S. M. Cabral De Menezes, R. Goodfellow, P. Granger, “NMR nomenclature: Nuclear spin properties and conventions for chemical shifts. IUPAC recommendations 2001”, Magn. Reson. Chem. 2002, 40, 489–505.
[3] M. Jaszunski, A. Antušek, P. Garbacz, K. Jackowski, W. Makulski, M. Wilczek, "The determination of accurate nuclear magnetic dipole moments and direct measurement of NMR shielding constants", Prog. Nuc. Magn. Res. Spec. 2012, 67, 49–63.
last changes: 07.11.2024, Imon Mandal and Hendrik Zipse, supported by the RTG 2620 on "Ion Pair Effects in Molecular Reactivity" questions & comments to: zipse@cup.uni-muenchen.de