8.3 Positional Averaging of Shielding Values
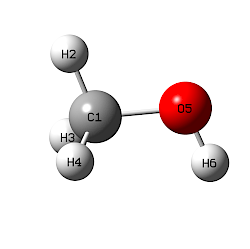
NMR spectroscopy is a comparatively slow spectroscopy compared to the rate of several dynamic intra- and intermolecular process. When calculating chemical shift values, these have to be adressed in an appropriate way. A simple example is methanol (CH3OH) used as a reactant, as a solvent for synthetic transformations, or (as methanol-d4, CD3OD) as NMR solvent.[1,2] The minimum energy structure of methanol obtained after geometry optimization is characterized by Cs symmetry as shown in Table 8.3.1. The shielding calculations are in this case performed with ORCA at the RI-MP2/pcSseg-2 level of theory. Shielding calculations performed at MP2 level often yield superior predictions as compared to hybrid DFT methods, and the very efficient RI-MP2 implementation available in ORCA makes this methodology available for comparactively large molecular systems. MP2 calculations are often (and in many programs by default) performed using the "Frozen Core (FC)" approximation, where non-valence electrons (e.g. the 1s electrons for carbon) are excluded from the correlation calculation. This is not meaningful for NMR shielding calculations and can be avoided by keywords such as "NoFrozenCore" in ORCA or "MP2(Full)" in Gaussian. The same also applies to calculations with double-hybrid methods such as B2PLYP. The pcSseg-2 basis set is a member of the pcSseg-n family of basis sets specifically developed by F. Jensen for the calculation of NMR shielding values.[3,4] When performing shielding calculations at RI-MP2 level, ORCA presents us with shielding values calculated in three different ways: (a) at RHF level with SCF densities, (b) at MP2 level with SCF densities, and (c) at MP2 level with relaxed densities. We will focus on the last set of shieldings here listed at the end of the ouput file as "CHEMICAL SHIELDING SUMMARY (ppm)". Shieldings for 1H are listed first in the order of appearance in the input coordinates. What is listed as nucleus 1 thus corresponds to hydrogen atom H2 in the input coordinates. The shielding of 28.111 ppm corresponds to that located in the symmetry plane of the system, while the following two values are for hydrogen atoms H3 and H4 located above and below the symmetry plane. These latter two values are identical at 28.044 ppm due to symmetry equivalencing. While the current calculation indeed reflects the Cs symmetry of the system in the molecular coordinates as well as the calculated shieldings, this is not always the case. Should shielding values for centers exchanged by symmetry operations not be identical then this has to be dealt with manually by simply averaging the shieldings over the respective positions.
Table 8.3.1. Input and relevant output file sections for NMR calculations with ORCA for methanol (CH3OH).
input file
! RHF RIJK RI-MP2 pcSseg-2 AutoAux TightSCF NMR
NoFrozenCore UseSym
%pal
nprocs 8
end
%scf
MaxIter 300
end
%maxcore 10000
* xyz 0 1
C -0.04641700 0.66017100 0.00000000
H -1.08664800 0.97773500 0.00000000
H 0.43835600 1.07136800 0.88940200
H 0.43835600 1.07136800 -0.88940200
O -0.04641700 -0.75227300 0.00000000
H 0.85977900 -1.06331300 0.00000000
*
%mp2
density relaxed # use relaxed MP2 density for NMR shift calculation
end
%eprnmr
NUCLEI = ALL H {SHIFT}
NUCLEI = ALL C {SHIFT}
end
|
output file
--------------------------------
CHEMICAL SHIELDING SUMMARY (ppm)
--------------------------------
Nucleus Element Isotropic Anisotropy
------- ------- ------------ ------------
1 H 28.111 7.720
2 H 28.044 8.620
3 H 28.044 8.620
5 H 31.615 19.977
0 C 142.018 78.492
system
|
The three protons in the methyl group of methanol can exchange their positions by rotation around the C-O bond. This rotation (and thus the exchange frequency of the three hydrogen positions) is much faster than the "NMR time scale" (whatever that may be in this particular case). In solution NMR measurements the hydrogen atoms H2, H3, and H4 will thus appear as a single signal centered at +3.49 ppm (in CDCl3 as the solvent, possibly split into a doublet by coupling to the adjacent OH group proton). This is an example of exchange averaging, where a fast dynamic process leads to averaging of the resonances over all positions involved in the exchange process. All we have to do to match this situation in shielding calculations is to average the calculated isotropic shieldings over the respective positions. For the methyl group in methanol we thus obtain an average 1H shielding value of (28.111 + 28.044 + 28.044)/3 = 28.066 ppm. At this level of theory, the 1H shielding in TMS amounts to 31.586 ppm. Taking the difference (that is, applying eq. (5)) yields a 1H chemical shift prediction for the methanol CH3 protons of +3.52 ppm, which is in impressively good agreement with the experimental value (measured in solution). While the shielding differences between the three interchanging protons are quite small in this particular case, they can become much larger (several ppm) for second row elements such as 13C or 19F.
Conformational averaging between several conformers of a given compound represents another case of exchange averaging. Under the condition of fast conformational exchange on the NMR time scale, the average shielding value for a given nucleus at a given temperature T will be influenced by both, the Boltzmann weight of a given conformer as well as its specific shielding value. A quantitative expression for the Boltzmann-averaged shielding values for a given nucleus is given in eq. (6).

Taking the example of n-butane, we obtain the trans conformation as the global minimum with relative energy 0.0 kJ/mol, and the slightly less stable (+3.8 kJ/mol) gauche conformer. The latter comes in two different absolute configurations, wich are mirror images of each other, and we thus have gtrans=1 and ggauche=2.
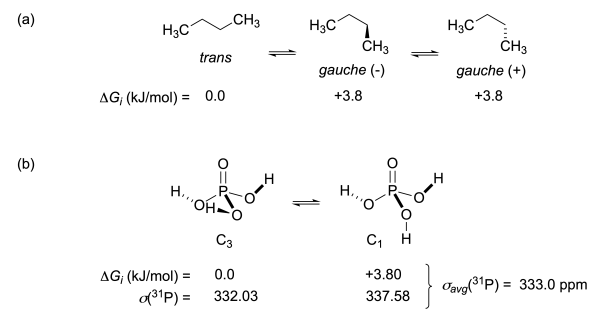
Figure 8.3.1. (a) Conformational analysis of n-butane. (b) Conformational analysis and isotropic shieldings for phosphoric acid (based on M06-2X/def2-TZVPP energies and RI-MP2/pcSseg-2//M06-2X/def2-TZVPP shieldings).
A second example is phosphoric acid, whose role as the zero reference of the 31P NMR scale will be discussed later. Gas phase conformational analysis of this system identifies two local minima, of which the C3-symmetric conformer serves as the global minimum with an isotropic shielding value of 332.03 ppm. This conformer comes in two different absolute configurations with respect to the central C3 axis and we thus have gC3 = 2. Only 3.80 kJ/mol higher we find a C1-symmetric conformer, where one of the three OH groups in the global minimum has flipped its orientation anti to the central P=O bond and where the isotropic shielding value is now significantly different at 337.58 ppm. This conformer also comes in two different absolute configurations and we thus have gC1 = 2. The Boltzmann-averaged 31P shielding value for phosphoric acid at T = 298.15 K calculated according to eq. (6) then amounts to 333.0 ppm.
References
[1] N. R. Babij, E. O. McCusker, G. T. Whiteker, B. Canturk, N. Choy, L. C. Creemer, C. V. De Amicis, N. M. Hewlett, P. L. Johnson, J. A. Knobelsdorf, F. Li, B. A. Lorsbach, B. M. Nugent, S. J. Ryan, M. R. Smith, Q. Yang, "NMR Chemical Shifts of Trace Impurities: Industrially Preferred Solvents Used in Process and Green Chemistry", Org. Process Res. Dev. 2016, 20, 661−667.
[2] G. R. Fulmer, A. J. M. Miller, N. H. Sherden, H. E. Gottlieb, A. Nudelman, B. M. Stoltz, J. E. Bercaw, K. I. Goldberg, “NMR Chemical Shifts of Trace Impurities: Common Laboratory Solvents, Organics, and Gases in Deuterated Solvents Relevant to the Organometallic Chemist”, Organometallics 2010, 29, 2176−2179
[3] F. Jensen, "Segmented Contracted Basis Sets Optimized for Nuclear Magnetic Shielding", J. Chem. Theory Comp. 2015, 11, 132−138.
[4] F. Jensen, "Basis Set Convergence of Nuclear Magnetic Shielding Constants Calculated by Density Functional Methods", J. Chem. Theory Comp. 2008, 4, 719−727.
last changes: 12.12.2024, Imon Mandal, and Hendrik Zipse, supported by the RTG 2620 on "Ion Pair Effects in Molecular Reactivity" questions & comments to: zipse@cup.uni-muenchen.de