Pauling bond order

The degree or order of bonding between two atoms cannot only be determined through analysis of the molecular wavefunction, but also through using the bond distance/bond order correlation established by Linus Pauling. This empirical scheme is particularly useful for comparing calculated and experimentally determined data, but also has some value as a "post factum" analysis method. The approach is based on the assumption that bond orders vary exponentially with bond distances. This can be expressed in a straightforward manner with equation (1):

n_x = n_o EXP((r_o - r_x)/c)             (1)

In equation (1) the bond order n_x of a bond of length r_x is a function of a reference bond of length r_o, whose bond order is defined as n_o. The constant c determines, how steeply the bond orders change with bond distances. Very frequently the reference bond distance is that of a single bond with n_o=1.0.
 

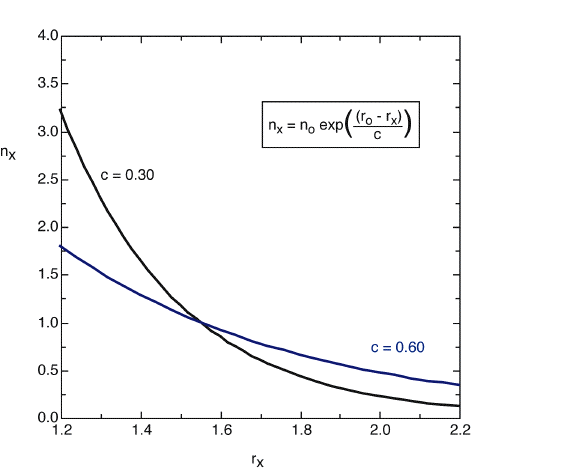
The original equation suggested by Pauling for single and double bonds uses a value of c = 0.3 (black line). For the analysis of bond orders in transition states this value leads to bond orders which are too small. For these structures a value of c = 0.6 appears to be more appropriate (blue line).

The calculation of bond orders n for ground state molecules will be demonstrated using ethylene, butadiene, and benzene as example. The following structural data have been calculated for these systems at the Becke3LYP/6-31G(d) level of theory (distances in pm):
 

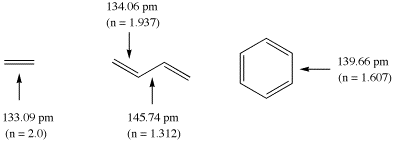
The double bond in ethylene is used here as the reference systems for bonds with bond order 2 at a bond length of 133.09 pm. Using Paulings original expression (c = 0.3) the bond orders in butadiene amount to 1.937 (C1-C2) and 1.312 (C2 - C3), and to 1.607 for benzene. It is clear from this example, that the calculated bond orders always depend on the chosen reference system!

references
L. Pauling,
"Atomic Radii and Interatomic Distances in Metals"
J. Am. Chem. Soc. 1947, 69, 542 - 553.

J. Wilkie, I. H. Williams,
"Transition-State Structural Variation in a Model for Carbonyl Reduction by Lactate Dehydrogenase: Computational Validation of Empirical Predictions Based upon Albery-More O'Ferrall-Jencks Diagrams"
J. Am. Chem. Soc. 1992, 114, 5423 - 5425.

K. N. Houk, S. M. Gustavson, K. A. Black,
"Theoretical Secondary Kinetic Isotope Effects and the Interpretation of Transition State Geometries. 1. The Cope Rearrangement"
J. Am. Chem. Soc. 1992, 114, 8565 - 8572.

S. S. Glad, F. Jensen,
"Kinetic Isotope Effects and Transition State Geometries. A Theoretical Investigation of E2 Model Systems"
J. Org. Chem. 1997, 62, 253 - 260.