Qualitative HMO-Theorie

Bevor wir die Molekülorbitale eines pi-Bindungssystems entsprechend den qualitativen Regeln von Heilbronner und Bock entwickeln können, ist es wichtig, das zu untersuchende pi-Bindungssystem bezüglich seiner Alternanz und seiner Symmetrie genauer zu klassifizieren.

Alternanz
Alternierende pi-Bindungssysteme sind solche, in denen sich die beteiligten Zentren so in einen besternten (*) und einen unbesternten (o) Satz unterteilen lassen, dass nur Bindungen zwischen Zentren unterschiedlicher Sätze (also zwischen besternten und unbesternten Zentren) resultieren. Hier einige Beispiele:

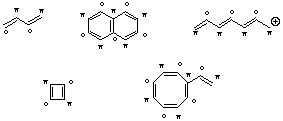
Nichtalternierende pi-Bindungssysteme hingegen enthalten mindestens eine Bindung zwischen Zentren aus dem gleichen Satz (also *-* oder o-o). Auch hierzu einige Beispiele:

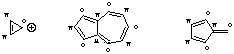
Symmetrie
Praktisch alle Systeme mit ausgedehntem pi-System sind eben; somit liegen alle Atome des Systems in einer Ebene, die auch gleichzeitig eine Spiegelebene für die pi-Molekülorbitale ist. Wird das pi-System nur aus p-Atomorbitalen aufgebaut, so sind sowohl alle Atomorbitale wie auch alle daraus aufgebauten Molekülorbitale antisymmetrisch bezüglich dieser Symmetrieebene. Diese Symmetrieeigenschaft wird bei der Ableitung der Molekülorbitale also nur bedingt hilfreich sein. Wichtige Symmetrieelement, die die Ableitung der Molekülorbitale erleichtern, sind Spiegelebenen oder zweizählige Symmetrieachsen, die orthogonal zum pi-Bindungssystem verlaufen. Dies sei nachfolgend am Beispiel von Butadien erläutert:

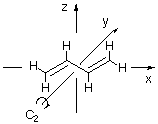
Alle Atome von Butadien liegen in diesem Fall in der xz-Ebene. Somit sind alle p-Orbitale, die das pi-Bindungssystem beschreiben, sowie alle Molekülorbitale des pi-Systems antisymmetrisch zur xz-Ebene. Neben dieser Symmetrieebene besitzt die gezeigte trans-Konformation von Butadien auch noch eine C₂-Achse, die in diesem Fall mit der y-Achse des Koordinatensystems zusammenfällt. Alle Molekülorbitale des pi-Systems müssen symmetrisch oder antisymmetrisch zu dieser C₂-Achse sein.

Regel A
Erstreckt sich ein pi-Elektronensystem über n Atomorbitale P_x (x=1,2,3, . . n), so besitzt es auch n Molekülorbitale Q_y (y=1,2,3, . . n).

Regel B
In der Linearkombination Q₁ des Molekülorbitals der niedrigsten Energie e₁ treten alle Atomorbitale P_x (x=1,2,3, . . n) mit dem gleichen Vorzeichen auf.

Regel C
Die Zahl der Knoten im Molekülorbital Q_y steigt im allgemeinen mit steigender Energie e_y.

Regel D
Bei linearen pi-Elektronensystemen ist die Zahl der Knoten im Molekülorbital Q_y gleich y-1.

Regel E
Bei cyclischen pi-Elektronensystemen mit n Zentren beträgt die Zahl der Knoten für die Paare entarteter Molekülorbitale Q_y und Q_-y jeweils 2y (y=1,2,3, . . (n-2/2)). Das nichtentartete Molekülorbital Q₀ niedrigster Energie e₀ besitzt keine Knoten, das oberste Molekülorbital Q_n/2 bei gerader Zentrenzahl n Knoten.

Regel F
In alternierenden pi-Elektronensystemen gehört zu jedem Molekülorbital Q_y ein Molekülorbital Q_(n-y+1) (y=1,2,3, . . n), welches sich von ersterem nur im Vorzeichen des kleineren besternten bzw. unbesternten Satzes von Atomorbitalen P_x unterscheidet.

Regel G
Alternierende pi-Elektronensysteme mit ungerader Anzahl von Atomorbitalen besitzen mindestens ein nichtbindendes Molekülorbital, dessen Energie gleich dem der ungestörten Atomorbitale ist. In der zugehörigen Linearkombination Q_nb sind die Koeffizienten des kleineren besternten bzw. unbesternten Satzes von Atomorbitalen identisch Null; im grösseren wechselt fortlaufend das Vorzeichen.

Regel H
Die Molekülorbitale Q_y eines symmetrischen pi-Elektronensystems müssen relativ zu den zweizähligen Symmetrieoperationen (Spiegelebenen, zweizähligen Achsen, Inversionszentren) entweder symmetrisch oder antisymmetrisch sein, d.h. zu einer irreduziblen Darstellung der betreffenden Gruppe gehören.

Regel I
Besteht ein pi-Elektronensystem ausschliesslich aus Kohlenstoffzentren (isokonjugiertes Modell), so ist die Distanz zwischen zwei aufeinander folgenden Knoten eines Moleküorbitals im allgemeinen etwa konstant.

Die Anwendung dieser Regeln soll am Beispiel von Butadien kurz demonstriert werden. Aus Regel A folgt, dass wir mit vier Moleküorbitalen für das pi-System rechnen müssen. Das energetisch niedrigstliegende dieser MOs ist durch Regel B vollständig bestimmt. Die nachfolgende Darstellung verwendet helle Kreise für positive Koeffizienten und dunkle Kreise für negative Koeffizienten:

Ist ein energetisch niedrig liegendes MO bekannt, so erlaubt uns Regel F die Ableitung eines energetisch höher liegenden MOs. Im Fall von Butadien kann aus der Struktur von Q₁ die Struktur von Q₄ abgeleitet werden.

Da es sich bei Butadien um ein Molekül mit alternierendem, linearen pi-System handelt, folgt aus Regel D, dass in MO Q₂ genau ein Knoten vorhanden sein muss. Da entsprechend Regel H alle MOs des pi-Systems von Butadien symmetrisch oder antisymmetrisch bezüglich der C₂-Achse sein müssen, ist auch Q₂ eindeutig festgelegt. Das noch fehlende MO Q₃ ergibt sich nach Regel F aus Q₂ durch Wechsel der Vorzeichen an allen besternten Zentren.

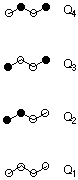
Eine Abschätzung der Orbitalenergien kann nun dadurch erreicht werden, dass für jedes MO die Anzahl von bindenden Beiträgen Z_BJ und antibindenden Beiträgen Z_AJ ermittelt und deren Differenz berechnet wird. Bindende Beiträge ergeben sich immer dann, wenn in einem MO Atomorbitale gleichen Vorzeichens miteinander verknüpft sind. Umgekehrt ergibt sich durch Vorzeichenwechsel zwischen zwei benachbarten Zentren ein antibindender Beitrag. Liegt ein Zentrum auf einem Knoten des pi-Systems, so sind Wechselwirkungen mit diesem Zentrum weder bindend noch antibindend. Für Butadien ergeben sich somit folgende Beiträge:

Für den einfachen Fall von Butadien entspricht die Abfolge der Orbitalenergien der Abfolge von Molekülorbitalen, die sich aus den qualitativen HMO-Regeln ergeben haben. Bei komplexeren Systemen ist dies nicht immer der Fall und die qualitative Abschätzung der Orbitalenergien kann in diesen Fällen als zusätzliches Hilfsmittel genutzt werden, um die relative Abfolge der Molekülorbitale festzulegen.

Literatur:
E. Heilbronner, H. Bock
"Das HMO-Modell und seine Anwendung, Band 1, 2 und 3"
2. Auflage, Verlag Chemie, 1978.